Our project was to provide the basic structure(geometry) of a 'realistic' looking tree. Our work was based on the paper by Jason Weber and Joseph Penn, "Creation and Rendering of Realistic Trees", available on the ACM site. The focus was on the California Black Oak, and Black Tupelo trees, since the paper provided the properties needed to create geometry similar to those types of trees.
Historically, when computer graphics simulations need natural looking scenes, they struggle to deal with plants and natural shapes. Often, bushes and trees are turned into billboarded planes that rotate with the camera, containing a texture map of the desired tree. This has the affect of removing the possibility for advanced shading or interactions with the tree, as it only has the geometry of a plane.
Other attempts at realistic trees are based on fractals. These can often lead to very artificial looking and predictable tree structures. In addition, the modeling process involves thinking in terms of complex mathematical constructs to affect tree construction.
The approach described by Weber and Penn was written in 1995, and in recent years seems to have become the standard for many games with libraries such as Speed-tree becoming available for reasonable hardware and price ranges.
The modeling part of the image synthesis pipeline was the main focus. Since the majority of the paper was on constructing the geometry, that was also our focus. We did not choose to go into the animation aspects for wind sway. The paper is also fairly agnostic to rendering systems, it could be used in a ray tracer or OpenGL just as easily.
At the highest level, a tree is a collection of parameters. These parameters are what affect the geometry of a tree, creating unique trees each time they are rendered. These parameters are used to simulate botanical elements of trees.
The parameters themselves are bundled into groups: one for overall tree information (lobes, shape, levels of recursion, etc) and one for each level of stems. The data for the parameters varies significantly as well. Some parameters are representative of distances, angles, counts, percentages (for probability calculations), and magnitudes of variation within each of these. For most parameters the user provides a base value (for example trunk length) and a variation which is how the system varries the trees generated each time. For example a user could define a trunk length of 10, and a trunk length variation of 5; the resulting tree would have a length in the range of 5 to 15.
Trees are constructed with stems and leaves. A stem is a collection of conical sections, that are either tapered to a full point, or truncated. A leaf is a hexagon shape found at the ends of the outer-most stems. Each tree is constructed of several levels of stems. The trunk is considered level 0, and branches off of the trunk are level 1, and so on. Typically trees defined using this process only use three levels of parameters, but it is possible to use more. Beyond three levels, however, the details tend to become so small that it is not worth the extra processing time to generate.
Trees, as mentioned before, are a collection of parameters. For implementation purposes this had to be a map to allow for quicker searching based on name value pairs. The following table outlines all of the parameters we had in our system:
| Parameter name(s) | Description |
|---|---|
| Shape | general tree shape id |
| BaseSize | fractional branchless area at tree base |
| Scale,ScaleV,ZScale,ZScaleV | size and scaling of tree |
| Levels | levels of recursion |
| Ratio,RatioPower | radius/length ratio, reduction |
| Lobes,LobeDepth | sinusoidal cross-section variation |
| Flare | exponential expansion at base of tree |
| 0Scale,0ScaleV | extra trunk scaling |
| 0Length,0LengthV, 0Taper | fractional trunk, cross-section scaling |
| 0BaseSplits | stem splits at base of trunk |
| 0SegSplits,0SplitAngle,0SplitAngleV | stems splits & angle per segment |
| 0CurveRes,0Curve,0CurveBack,0CurveV | curvature resolution and angles |
| 1DownAngle,1DownAngleV | main branch: angle from trunk |
| 1Rotate,1RotateV,1Branches | spiraling angle, # of branches |
| 1Length,1LengthV,1Taper | relative length, cross-section scaling |
| 1SegSplits,1SplitAngle,1SplitAngleV | stem splits per segment |
| 1CurveRes,1Curve,1CurveBack,1CurveV | curvature resolution and angles |
| 2DownAngle,2DownAngleV | secondary branch: angle from parent |
| 2Rotate,2RotateV,2Branches | spiraling angle, # of branches |
| 2Length,2LengthV, 2Taper | relative length, cross-section scaling |
| 2SegSplits,2SplitAngle,2SplitAngleV | stem splits per segment |
| 2CurveRes,Curve,2CurveBack,2CurveV | curvature resolution and angles |
| 3DownAngle,3DownAangleV | tertiary branch: angle from parent |
| 3Rotate,3RotateV,3Branches | spiraling angle, # of branches |
| 3Length,3LengthV, 3Taper | relative length, cross-section scaling |
| 3SegSplits,3SplitAngle,3SplitAngleV | stem splits per segment |
| 3CurveRes,3Curve,3CurveBack,3CurveV | curvature resolution and angles |
| Leaves,LeafShape | number of leaves per parent, shape id |
| LeafScale,LeafScaleX | leaf length, relative x scale |
| AttractionUp | upward growth tendency |
| PruneRatio | fractional effect of pruning |
| PruneWidth,PruneWidthPeak | width, position of envelope peak |
| PrunePowerLow,PrunePowerHigh | curvature of envelope |
These parameters were built into our Tree objects and a then pulled appart by our TreeRenderer. The TreeRenderer is the heart of the implementation, but only works because of the supporting utilties for generating meshes, cones, and performing other graphics oeprations.
The basic algorithm is recusive. Starting with the trunk, it recursively descends along the trunk generating a conic section each time. The number of times a stem is iterated down depends on the `CurveRes` parameters. At each step, there is a probability that the algorithm will descend into another, seperate recursive process for generating the next level of branches, assuming that it is not at the last level.
As these conic sections are generated, they are transformed by a current transformation matrix that is passed along during each phase of recursion and slightly altered at each step. As a result, all the sections geometry ends up in the correct location relative to the base of the tree. This allowed us put all the geometry into a larger collection to send it to the video-card using Vertex Buffer Objects (VBOs). This was important because, even though one of the goals of the paper was to create very fast rendering trees, the number of vertices can grow very large. Using those vertices using OpenGL immediate mode would have made the system run incredibly slow.
The manipulations for stem curvature, splitting, and branching, as mentioned, are all done using matrix transformations. The values used are derived from the equations in the paper. However, since some of the details for were not explained as clearly as to make them straight-forward to implement, we have taken some liberties in our version. For example, generating branches on the trunk (the first level of branches) is straight forward. You can determine an approximate number of branches per recursive step and then distribute those throughout that conic section. For generating second level branches, it isn't as straightforward. The number of branches at that level is distributed across all of the first level. So, in the end, the probability per segment becomes a factor of two levels of probability, we think. To avoid screwing up the caclulations we implemented a more straight forward, less accruate model where a child branch is created one time per parent segment.
One major difference between the paper, and our implementation is geometry generation. We build cones, and add them to a mesh. The paper describes a process where the end points of each one are recorded, then they go back and 'connect the dots.' While the second approach is more visually appealing, because there are no 'cracks' in the stems, it is much more diffiult to compute. For example, the paper authors discuss when rotations are applied to a section of stem the connections could end up being 180 or so degrees out of alignment creating a very inaccurate, twisted look. They resolve this, to a degree. If we were to implement the same logic, we wouldn't have made it as far as we have.
The generation of meshes in our project is fairly interesting. The conic sections are all individual meshes. Meshes can be transformed, obviously, by matrices. These meshes can be added together to generate a new, combined mesh. The combined mesh can be added with others to generate even larger meshes. The layout of a mesh is essentially a handful of lists, one for vertices, edges, texture coordinates, and normals for each vertex. A mesh can be converted into a VBO at anytime, which converts the lists into arrays of raw data which can be injected into the video-card very quickly. After a mesh has been converted to a vertex buffer, however, it cannot easily reuploaded to the video-card without a complete recreation of the vertex buffer. If we were to implement wind sway, we would potentially have to re-think some of our mesh design so that it would be easier to manipulate the raw data.
There are many other aspects to our system that do not have much influence on the generation of trees, for example input management required writing a system of event-driven listeners so that input from SDL could be converted to CEGUI, or interpreted in our own application specific usage.
* Technical Details -- Describe the algorithms, data structures, and techniques used.The application we built is focused on 'designing' trees. It lets users build a tree using a list of parameters. The parameters are fixed in the GUI up to three levels of detail (3 levels branches beyond the trunk).
The application defaults to the parameters described in the paper for a California Black Oak. There is no way to load any other tree at runtime, and there is only one fully described tree in code, the Black Tupelo. The user can, however, modify every property that is used to generate the tree making it possible to generate whatever apperance they desire.
Editing the parameters requires simply clicking in an edit box, changing the numeric values, and pressing the "Render" button on the top. After calculating the geometry, which can take a significant amount of time, the new tree is displayed in the environment. This tree is at the 'highest' detail setting that the paper's algorithm can produce. Since we have not implemented the levels of detail aspects, it is not possible to view what those levels would produce in our application.
The user can 'explore' the tree that is generated by left clicking in the environment area and moving the mouse around. This has the effect of rotating the camera around a focus point along the Y (green) axis. Using the mouse wheel has the effect of zooming the camera in and out towards that focus point. Right clicking and dragging the mouse vertically has the effect of moving the focus poitn up and down the Y (green) axis.
The following images show several different variations on trees to get a sense of how the program works.
The first two images show samples of what the default parameters can generate. They capture the basic tree structure of a trunk with two levels of branches attached to it. The images show the same tree at two different angles.
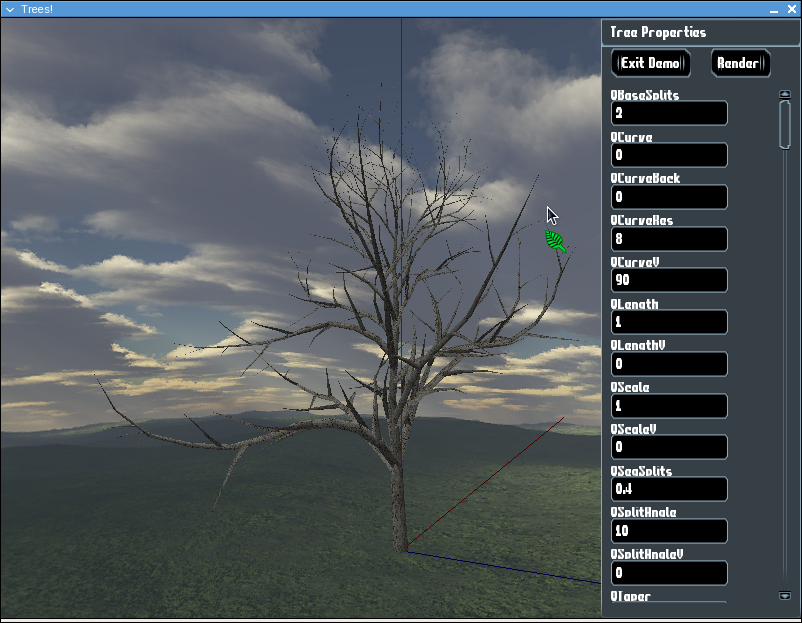

The following shows another variation of the original parameters, this time using a different shape (shape #0). This shape forms essentially a cone, with a base towards the ground. Shapes affect the length of branches as well as the angle that they are spawned out of a parent. In the case of a cone, the branches closer to the bottom are longer, and those near the top are shorter.
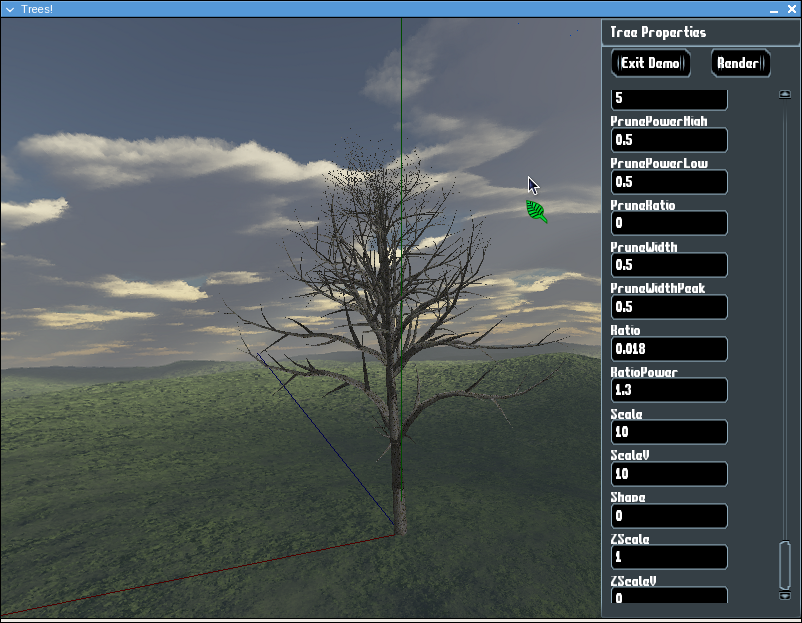
The following image shows a tree with an inverse conical shape (shape id #1). This is the opposite of conical, instead of getting smaller towards the top, it gets bigger.
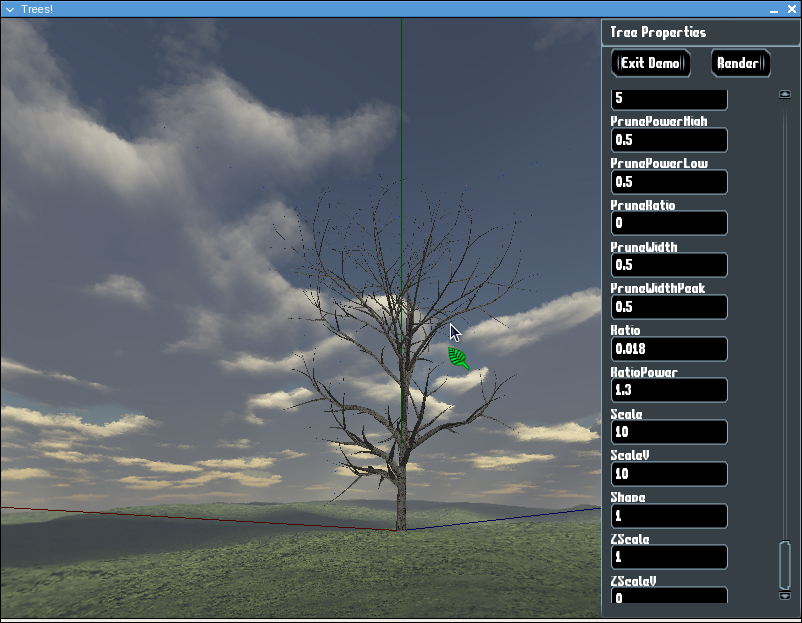
The value of the "Levels" parameter affects the depth of recursion when building branches. That is, how many generations of branches to generate, not their length. The default is 3 for this tree. Since we do not correctly calculate probalistic branches for anything beyond the first level of branches, we had to actually make the rendering go to one less than the specified level. This is because our chosen approach always generated branches, even if there was a specified value of 0 for the probability. As a result, any blank values in parameters caused very large scaling issues.
The following image shows the same tree parameters as the previous, with the levels set to 2, instead of 3. The effect is a much more 'bare' tree.

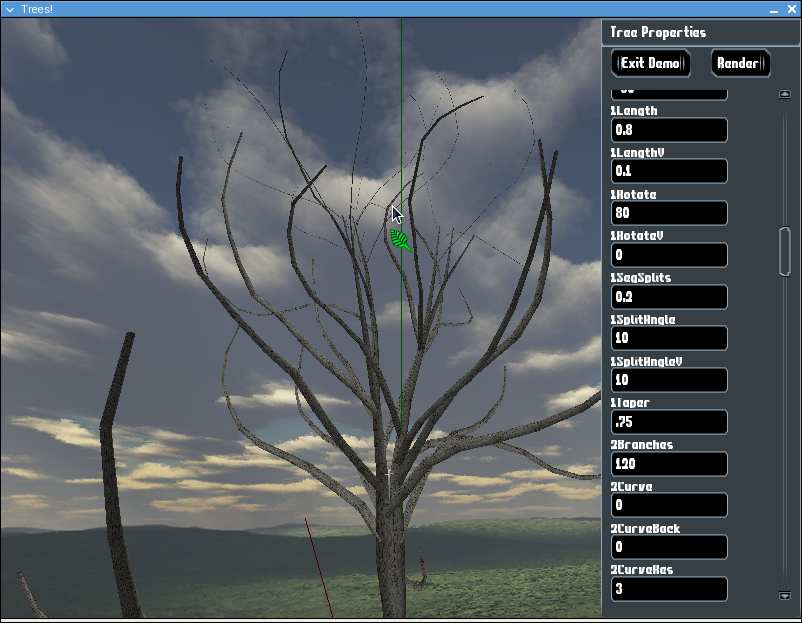
Each stem has a taper factor. The tapering of a stem in the most simple case, is to a point at the end (this is when taper is set to 1 for a given level). By default, the trunk of this tree has a taper of .95, resulting in a stem that does not come to a complete point, but close to it. Values above 1 cause the shape to repeat, forming 'plates' similar to that of a palm tree. Values above 2 are supposed to generate hemispherical tapering at the ends. Our implementation does not seem to work correctly for cases above 1, but it does work for those below it.
The last image shows a tree with the first level branches tapering set to .75, and leaving obvious, non-pointed stems.
* Results -- The 3D Rendering and / or screen shots of the application. If the project is an application you should include user documentation here.
Obvious future work includes implemented more of the details and fixing issues in our current implementation. Aside from correcting issues and adding more of the paper's features, we would like to implement importing and exporting capabilities.
Aspects of the paper that we have not implemented, and would like to include: leaves, wind sway, pruning, lobes, vertical attraction, and degredation at range.
Leaves are the only other shape that we would have to deal with, and form the outer layer of the tree. They are constructed using hexagons that are scaled to various ratios. Leaves would tremendously help with realism, and also optimizations as they can be used to 'hide' small branches when reducing the number of triangles. The main difficulties in implementing this are the probability calculations for determining when to place them, and dealing with them as a seperate mesh (since they would need seperate textures). Finding good textures for this would be important as well as leaves are one of the more unique identifiers for a particular type of tree.
Wind sway is an animation feature mapping elastic movement over time. As stems get higher up the tree, the amount of deflection is increased more than those that are lower, to simulate the flexability of thinner branches. The amount of force applied to the tree is uniform, but configurable through the wind-speed parameter.
Pruning is the last shape that a tree can use. Unlike the other shapes, the pruning shape is determined by functions that take 4 parameters. These parameters are used in the shape equations to allow users to define more interesting looking trees that are not as easy to acomplish with the standard shapes. For example, a curved conical shape, with hemispherical bottom is possible with a pruning envelope, but not possible using the standard simple shapes. Essentially, it offers more control to the user over the shape of the tree.
Lobes are structures on the base of a tree that, with addition to flaring, help give the apperance of a root structure above ground level. The lobes are perturbed from the base of the tree, and blended together to generate a cross section that is non-circular. An example is a cyprus tree or cactuses with ridges, which are otherwise hard to model accurately without lobes.
Vertical attraction is an effect for both stems and leaves. Currently, though the stems seem to rotate upwards, this is only an effect of the rotation parameters defined. It is possible to have rotations that do not go upwards. In nature, plants tend to seek light. Since most of their light comes from the sun they tend to bend upwards, or towards the brighest light they can find, if they are in a shaded environment. By orienting our stems and leaves towards light sources, it removes some of the 'randomness' that will cause them to come out in odd directions, and improve the image quality as more light is reflected correctly.
Degredation at range, as mentioned is the ability of the system to re-generate the same tree, with lower detail. This allows the tree to be scaled to a smaller size with reduce complexity. The result is that as the user navigates some environment, the smaller a tree is in the distance, the less computational resources are needed to draw it. This should also be seamless, or it will distract the user as it jumps between levels. To accomplish this, the paper describes merging segments and rendering stems as less complex objects (wires, planes, etc).
One of the feature sets would be importing and exporting data. This would include both mesh information and tree parameters. Exporting meshes would allow us to use the tool to generate trees, then once we make a good looking tree, export it and use it in some other program such as blender for making a scene or a game environment. Exporting and importing parameters would allow designers to start with a basic tree, modify it, and save it out. This would speed up the process of making variations to a class of trees and allow people to go back to previous trees quickly and easily. It would also be useful for testing as it would let us make test cases with odd tree parameters to make sure they still work after making changes.
* Future Enhancements -- If you/your team were to continue working on this project, what would you like to add/fix.
The system is not easily 'installed' because the paths to data files are all assuming that it is running from within a source directory. So, the best way to run the program is rom within the source, which also makes it easier to end up working on the source and making the program more interesting -- rather than just using it.
There are two ways to build our project. The first is to use CMake to generate a build environment. The second is to use our provided Visual Studio project files, which were not generated by CMake, and we have not used much (meaning it may or may not work...)
A clean copy of the source should look something like:
trees/ trees/src trees/data trees/include trees/libs
I tend to add a build directory, "trees/build" which is where I have cmake generate its output using:
cmake ..
This will generate the makefiles to build the project, and check to make sure you have the required libraries -- SDL, SDL_image, and CEGUI. Once the Makefiles are generated, run make. Once the build finishes, from the trees/ directory, run:
build/src/Trees
With the cmake build, you should be able to generate project files for many IDEs such as Eclipse CDT or Visual Studio using CMake, but I haven't tried this yet.
The executable takes an optional argument, a path to a texture file for the bark.
Even though we use cmake, we didn't have the ability to install it on lab machines, so we manually created a Visual Studio project to build the project.
The version that was put in the MyCourse's dropbox includes all dependencies, but anything else based on the SVN repository does not have the DLLs, though it has the include and library files needed to build in Visual Studio.
This should enable building, but to run requires downloading the DLL files. For SDL download the SDL 1.2.13 windows release here, and SDL_image from here. Copy these DLLs into the trees directory (at the same level as the 'src' directory). For CEGUI, download the latest SDK from here and extract the DLLs to the same place.
To build, and run the project, just open the .sln in Visual Studio 2008 and run it.
The code was put in a mycourses dropbox, as a zip. All the code is also availble in SVN at:
http://svn.emarcotte.com/cg2/trees